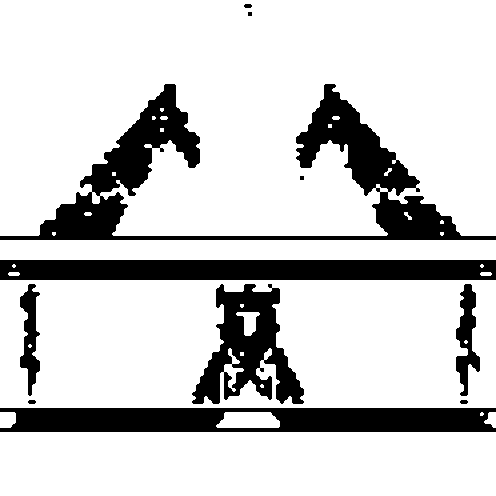
About
Tomography (from greek tomos = slice or section and grapho= to write or to describe) is an image reconstruction method by using sections generated from any kind of penetrating wave passing through a not accessible or not visible object..
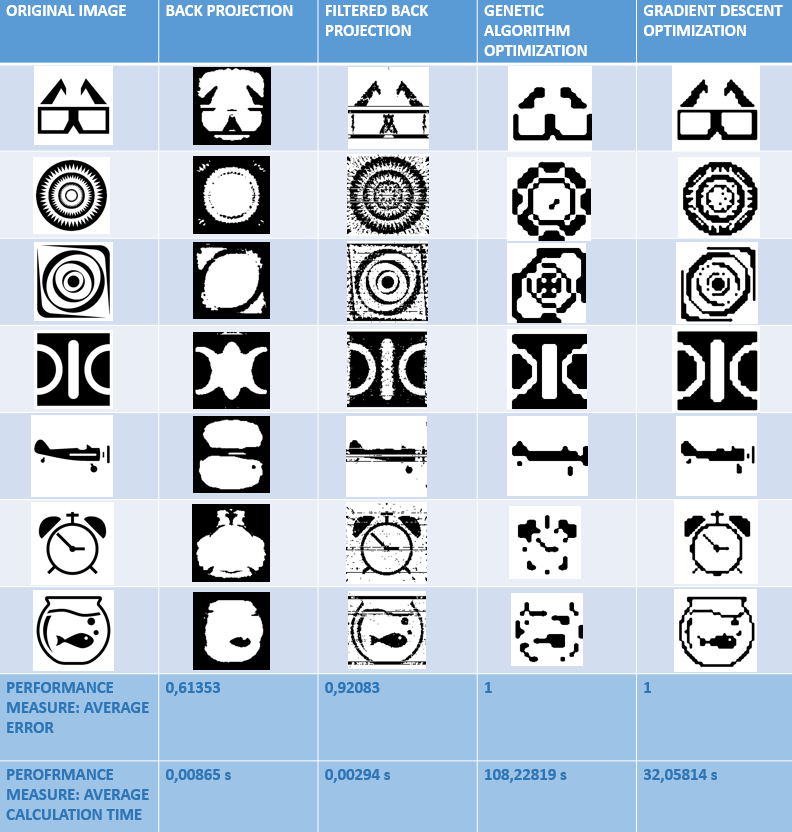
Binary image is an image whose pixels have only two possible intensity values: 0 (black) and 1 (white). It is useful because of an easy separation of an object from the background.
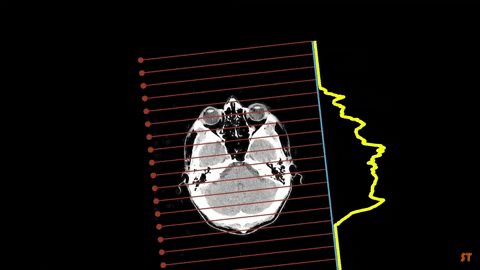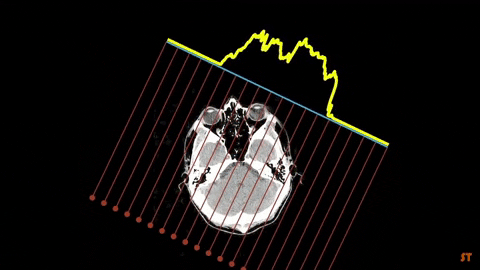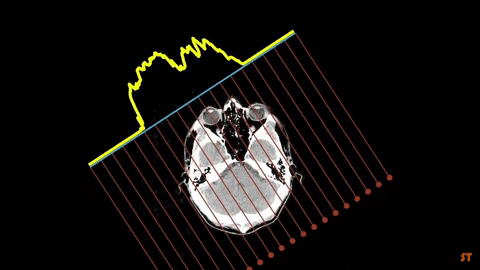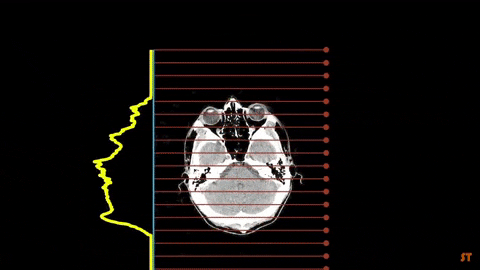

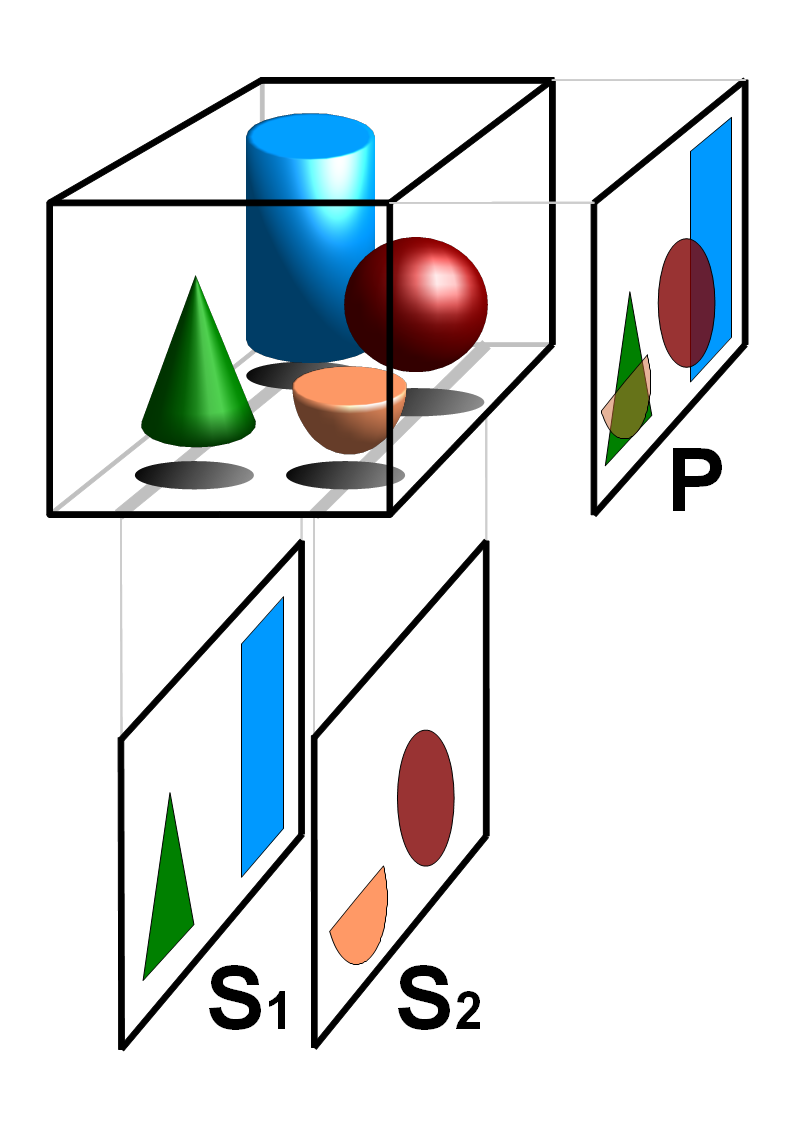
Binary Tomography (BT) deals with the reconstruction of binary images by using a limited number of their projections. It is a special case of Discrete Tomography (DT), an image reconstruction technique dealing with a finite discrete set of functions. With DT, reconstruction of an image is possible with a much smaller dataset than for the Computerized Tomography (CT).
Binary Tomography reconstruction methods require data from at least two or even more projection directions. However, the problem with binary image reconstruction is that several binary images can have the same projections especially when only one or two projections are given, which makes the problem undetermined. This is why some additional a priori information is needed in the reconstruction process, for example geometrical or material descriptors of the observed image or energy functions.
The basic BT reconstruction problem can be represented by a set of linear equations written in matrix form as
A u = b, A ∈ RM×N, u ∈ {0, 1}N, b ∈ RM
where:
A is the projection matrix whose each row represents one projection ray,
b is the projection vector containing the projected values,
u is the vector of the unknown binary image to be reconstructed.
The reconstruction problem deals with finding the solution vector u from the linear system of equations, where the projection matrix and the projection vector are given. As the system is in most cases underdetermined (N > M), some additional regularization is needed to achieve satisfactory reconstruction of the original images.